個人的な生成プロセスでgemini-2.5-pro-exp-03-25に試しに生成させた紙飛行機シミュレーターです。想像を超えるものが出力されたので、びっくりしてしまいました。私が直接指示したのは”Pythonで紙飛行機の飛行シミュレーター”のみのファーストテイクです。出力されたコードを記載しておきますので、streamlitを扱える方は気楽にお試しください。
# paper_plane_simulator.py
import streamlit as st
import numpy as np
import matplotlib.pyplot as plt
# --- 定数 ---
G = 9.81 # 重力加速度 (m/s^2)
RHO = 1.225 # 標準空気密度 (kg/m^3) at sea level
# --- アプリケーションのタイトル ---
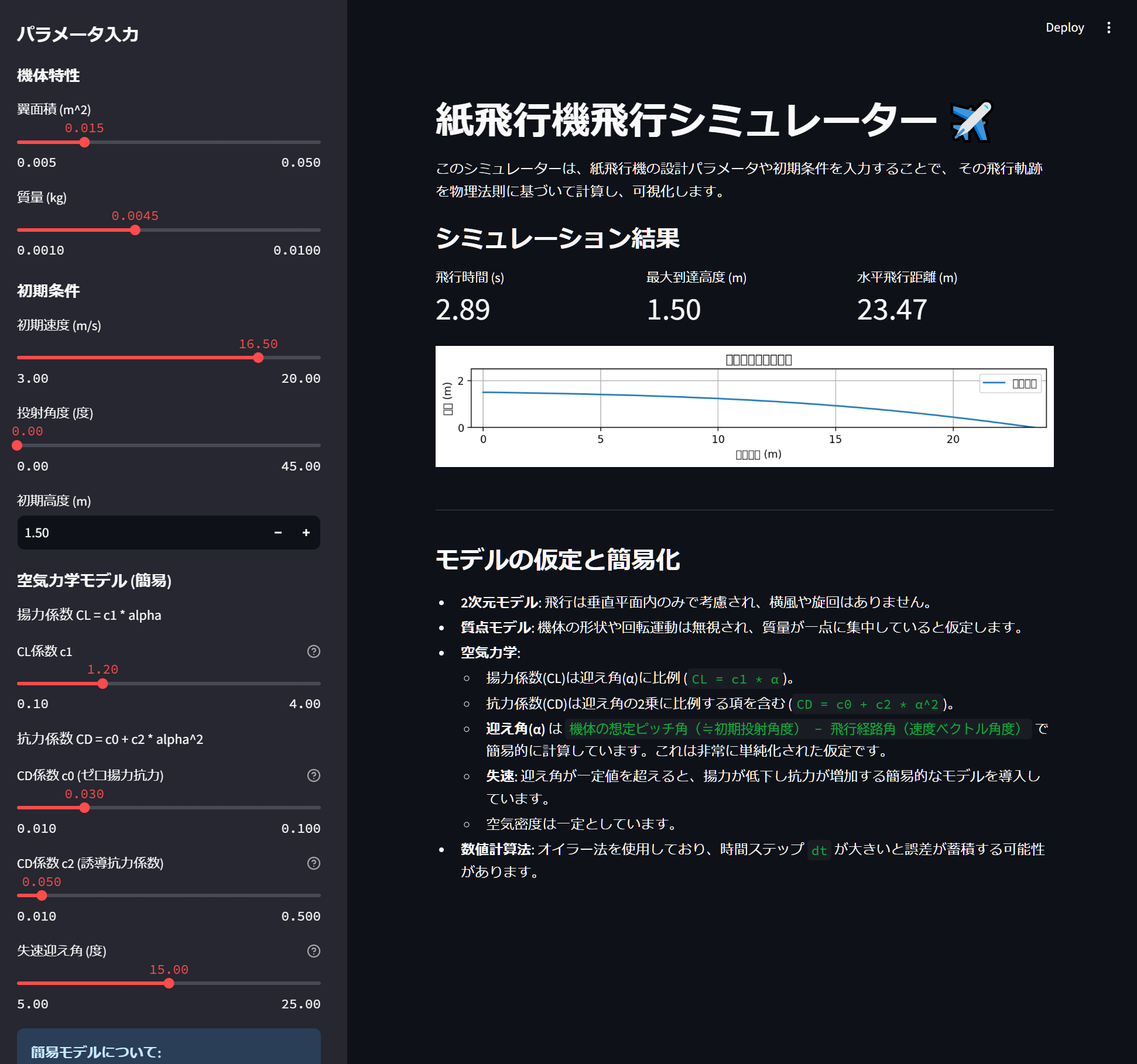
st.title("紙飛行機飛行シミュレーター ✈️")
st.write("""
このシミュレーターは、紙飛行機の設計パラメータや初期条件を入力することで、
その飛行軌跡を物理法則に基づいて計算し、可視化します。
""")
# --- パラメータ入力 (サイドバー) ---
st.sidebar.header("パラメータ入力")
# 物理的特性
st.sidebar.subheader("機体特性")
area = st.sidebar.slider("翼面積 (m^2)", min_value=0.005, max_value=0.05, value=0.015, step=0.001, format="%.3f")
mass = st.sidebar.slider("質量 (kg)", min_value=0.001, max_value=0.01, value=0.005, step=0.0005, format="%.4f")
# 初期飛行条件
st.sidebar.subheader("初期条件")
initial_velocity = st.sidebar.slider("初期速度 (m/s)", min_value=3.0, max_value=20.0, value=10.0, step=0.5)
launch_angle_deg = st.sidebar.slider("投射角度 (度)", min_value=0.0, max_value=45.0, value=10.0, step=1.0)
initial_height = st.sidebar.number_input("初期高度 (m)", min_value=0.0, value=1.5, step=0.1)
# 空気力学モデルパラメータ (簡易モデル)
st.sidebar.subheader("空気力学モデル (簡易)")
st.sidebar.write("揚力係数 CL = c1 * alpha")
c1 = st.sidebar.slider("CL係数 c1", min_value=0.1, max_value=4.0, value=2.0, step=0.1, help="揚力係数と迎え角の比例係数。値が大きいほど揚力が大きくなる。")
st.sidebar.write("抗力係数 CD = c0 + c2 * alpha^2")
c0 = st.sidebar.slider("CD係数 c0 (ゼロ揚力抗力)", min_value=0.01, max_value=0.1, value=0.03, step=0.005, format="%.3f", help="迎え角ゼロでの抗力係数(形状抵抗など)。")
c2 = st.sidebar.slider("CD係数 c2 (誘導抗力係数)", min_value=0.01, max_value=0.5, value=0.05, step=0.005, format="%.3f", help="揚力の発生に伴う抗力(誘導抗力)の係数。")
stall_angle_deg = st.sidebar.slider("失速迎え角 (度)", min_value=5.0, max_value=25.0, value=15.0, step=0.5, help="これ以上の迎え角になると揚力が低下し、抗力が増大すると仮定する角度。")
st.sidebar.info("""
**簡易モデルについて:**
- 迎え角 (alpha) は、機体の進行方向と投射角度から簡易的に計算されます。
- 空気力学モデルは非常に単純化されており、実際の飛行とは異なる場合があります。
- **注意:** 適切なパラメータが見つからない場合、飛行軌道が不自然になることがあります。
""")
# --- シミュレーション制御 ---
st.sidebar.subheader("シミュレーション制御")
max_time = st.sidebar.number_input("最大シミュレーション時間 (s)", min_value=1.0, max_value=60.0, value=10.0, step=0.5)
dt = st.sidebar.select_slider(
"時間ステップ dt (s)",
options=[0.001, 0.002, 0.005, 0.01, 0.02, 0.05],
value=0.01,
help="計算の時間刻み幅。小さいほど精度が上がるが、計算時間が長くなる。"
)
# --- シミュレーションエンジン (プレースホルダ) ---
def simulate_flight(params):
# ここにシミュレーションロジックが入る
# 今はダミーデータを返す
x = np.linspace(0, 10, 100)
y = -0.1 * (x - 5)**2 + 3.0
y = np.maximum(y, 0) # 地面以下にはいかない
time_flight = 3.0
max_height = 3.0
distance = 10.0
error_message = None
# ---- !!! ここから物理シミュレーションを実装します !!! ----
# パラメータ展開
area = params['area']
mass = params['mass']
v0 = params['initial_velocity']
angle0_rad = np.radians(params['launch_angle_deg'])
y0 = params['initial_height']
c1 = params['c1']
c0 = params['c0']
c2 = params['c2']
stall_angle_rad = np.radians(params['stall_angle_deg'])
max_t = params['max_time']
dt = params['dt']
# 初期状態
x_pos = [0.0]
y_pos = [y0]
vx = [v0 * np.cos(angle0_rad)]
vy = [v0 * np.sin(angle0_rad)]
t = [0.0]
# オイラー法による数値積分ループ
current_t = 0.0
while current_t < max_t:
# 現在の状態
current_vx = vx[-1]
current_vy = vy[-1]
current_x = x_pos[-1]
current_y = y_pos[-1]
# 地面に到達したら終了
if current_y < 0 and current_t > 0.1: # 最初のステップでの誤判定を防ぐ
# 線形補間で着地位置と時間を推定(簡易版)
t_ratio = -y_pos[-2] / (current_y - y_pos[-2]) if (current_y - y_pos[-2]) != 0 else 0
final_t = t[-2] + t_ratio * dt
final_x = x_pos[-2] + t_ratio * (current_x - x_pos[-2])
# 結果を上書き
t[-1] = final_t
x_pos[-1] = final_x
y_pos[-1] = 0.0
break
# 速度と飛行経路角
v = np.sqrt(current_vx**2 + current_vy**2)
if v < 1e-6: # 速度がゼロに近い場合は計算を打ち切る
error_message = "速度がほぼゼロになりました。"
break
gamma = np.arctan2(current_vy, current_vx) # 飛行経路角 (rad)
# 簡易的な迎え角 alpha の計算
# ここでは非常に簡易的に、機体の姿勢は常に投射角度に固定されていると仮定する
# 実際の飛行では機体姿勢も変化するが、簡単のため省略
# alpha = angle0_rad - gamma
# ----> より簡易的に「機体角度」は初期投射角度のままとする案(pitch_angle = angle0_rad)
alpha = angle0_rad - gamma # これはより現実に近いかも?機体軸と速度ベクトルのなす角
# ----> さらに簡易的に、alphaは飛行経路角 gamma に依存させず、一定と考えるか?
# ----> もしくは、水平に近いと仮定して alpha ≒ 投射角度(pitch angle) とみなす?
# 指示書モデルに基づき、alpha = (投射角度相当) - 飛行経路角 としてみる
# 補正:αが負にならないように調整(常に上向きの揚力を仮定する場合。簡易モデルとして許容?)
# alpha = max(0, angle0_rad - gamma) # これは物理的ではないかも
# --- 再考 ---
# α は 機体基準線 (例:翼弦線) と 空気流の相対角度
# 簡易モデルでは、機体の姿勢角(θ=pitch angle)を一定(=投射角度 angle0_rad)と仮定することが多い
# 空気流の方向は速度ベクトル (-vx, -vy) の方向、つまり -gamma
# よって、alpha = θ - gamma = angle0_rad - gamma が一つの妥当な簡易モデル
# CL, CD の計算 (失速を考慮)
if abs(alpha) <= stall_angle_rad:
cl = c1 * alpha
cd = c0 + c2 * alpha**2
else:
# 失速状態:CLは低下し、CDは増大すると仮定 (簡易モデル)
# 低下・増大の度合いは調整が必要
cl_stall = c1 * stall_angle_rad * 0.7 # 例: 失速角での70%に低下
cd_stall = c0 + c2 * stall_angle_rad**2 + 0.1 # 例: 抗力が大幅増
if alpha > stall_angle_rad:
cl = cl_stall
cd = cd_stall
else: # 負の大きな迎え角の場合
cl = -cl_stall # 負の揚力
cd = cd_stall
# CL/CDの急変は不安定要因になる可能性がある点に注意
# 動圧
q = 0.5 * RHO * v**2
# 揚力(L)と抗力(D)
lift = q * area * cl
drag = q * area * cd
# 力の成分 (x, y)
# 重力
fgx = 0.0
fgy = -mass * G
# 空気力 (Lift/Drag座標系からx/y座標系へ変換)
# Lはvに垂直、Dはvと逆向き
fax = -drag * np.cos(gamma) - lift * np.sin(gamma)
fay = -drag * np.sin(gamma) + lift * np.cos(gamma)
# 合力
fx = fgx + fax
fy = fgy + fay
# 加速度
ax = fx / mass
ay = fy / mass
# 次のステップの速度と位置 (オイラー法)
next_vx = current_vx + ax * dt
next_vy = current_vy + ay * dt
next_x = current_x + current_vx * dt # 微修正: current_vx * dt を使うのが素直
next_y = current_y + current_vy * dt
# データを記録
vx.append(next_vx)
vy.append(next_vy)
x_pos.append(next_x)
y_pos.append(next_y)
t.append(current_t + dt)
# 時間更新
current_t += dt
# 念のための発散防止 (大きなステップなど)
if not (np.isfinite(next_x) and np.isfinite(next_y)):
error_message = "計算が発散しました。時間ステップdtを小さくするか、パラメータを見直してください。"
# 途中までのデータで結果を返す
x_pos = x_pos[:-1]; y_pos = y_pos[:-1]; t = t[:-1]; vx = vx[:-1]; vy = vy[:-1]
break
# 最終的な計算結果の抽出
x_arr = np.array(x_pos)
y_arr = np.array(y_pos)
time_flight = t[-1]
max_height = np.max(y_arr) if len(y_arr) > 0 else y0
distance = x_arr[-1] if len(x_arr) > 0 else 0.0
# ゼロ除算等で NaN になった場合のエラーハンドリング
if np.isnan(time_flight) or np.isnan(max_height) or np.isnan(distance):
error_message = "計算結果が無効な値になりました。パラメータを確認してください。"
# 空の結果を返す
return np.array([]), np.array([]), 0.0, 0.0, 0.0, error_message
return x_arr, y_arr, time_flight, max_height, distance, error_message
# --- シミュレーション実行ボタン ---
if st.sidebar.button("シミュレーション開始"):
# パラメータを辞書にまとめる
params = {
'area': area,
'mass': mass,
'initial_velocity': initial_velocity,
'launch_angle_deg': launch_angle_deg,
'initial_height': initial_height,
'c1': c1,
'c0': c0,
'c2': c2,
'stall_angle_deg': stall_angle_deg,
'max_time': max_time,
'dt': dt
}
# スピナー表示で計算中を示す
with st.spinner('飛行軌跡を計算中...'):
try:
x_traj, y_traj, flight_time, max_h, flight_dist, error_msg = simulate_flight(params)
if error_msg:
st.error(f"シミュレーションエラー: {error_msg}")
elif len(x_traj) == 0:
st.warning("シミュレーション結果が空です。パラメータを確認してください。")
else:
st.subheader("シミュレーション結果")
# 結果の数値表示
col1, col2, col3 = st.columns(3)
col1.metric("飛行時間 (s)", f"{flight_time:.2f}")
col2.metric("最大到達高度 (m)", f"{max_h:.2f}")
col3.metric("水平飛行距離 (m)", f"{flight_dist:.2f}")
# 飛行軌跡グラフ
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x_traj, y_traj, label="飛行軌跡")
ax.set_xlabel("水平距離 (m)")
ax.set_ylabel("高度 (m)")
ax.set_title("計算された飛行軌跡")
ax.set_aspect('equal', adjustable='box') # アスペクト比を1:1に
ax.grid(True)
# x,yの表示範囲を自動調整しつつ、yは0以上を確保
ax.set_xlim(left=0)
ax.set_ylim(bottom=0)
min_data_bound_x = np.min(x_traj) if len(x_traj) > 0 else 0
max_data_bound_x = np.max(x_traj) if len(x_traj) > 0 else 1
min_data_bound_y = np.min(y_traj) if len(y_traj) > 0 else 0
max_data_bound_y = np.max(y_traj) if len(y_traj) > 0 else 1
ax.set_xlim([min(0, min_data_bound_x-0.5), max_data_bound_x + 0.5])
ax.set_ylim([0, max(max_data_bound_y + 0.5, initial_height + 1.0)]) # 初期高度も見切れないように
ax.legend()
st.pyplot(fig)
except Exception as e:
st.error(f"予期せぬエラーが発生しました: {e}")
# デバッグ用にトレースバックも表示する (開発中のみ)
# import traceback
# st.error(traceback.format_exc())
else:
# 初期表示またはパラメータ変更時
st.info("左のサイドバーでパラメータを調整し、「シミュレーション開始」ボタンを押してください。")
# プレースホルダーグラフ表示(オプション)
fig, ax = plt.subplots()
ax.set_xlabel("水平距離 (m)")
ax.set_ylabel("高度 (m)")
ax.set_title("飛行軌跡 (シミュレーション待機中)")
ax.grid(True)
ax.set_xlim(0, 10)
ax.set_ylim(0, 5)
st.pyplot(fig)
# --- 補足説明 ---
st.markdown("""
---
### モデルの仮定と簡易化
* **2次元モデル**: 飛行は垂直平面内のみで考慮され、横風や旋回はありません。
* **質点モデル**: 機体の形状や回転運動は無視され、質量が一点に集中していると仮定します。
* **空気力学**:
* 揚力係数(CL)は迎え角(α)に比例 (`CL = c1 * α`)。
* 抗力係数(CD)は迎え角の2乗に比例する項を含む (`CD = c0 + c2 * α^2`)。
* **迎え角(α)** は `機体の想定ピッチ角(≒初期投射角度) - 飛行経路角(速度ベクトル角度)` で簡易的に計算しています。これは非常に単純化された仮定です。
* **失速**: 迎え角が一定値を超えると、揚力が低下し抗力が増加する簡易的なモデルを導入しています。
* 空気密度は一定としています。
* **数値計算法**: オイラー法を使用しており、時間ステップ `dt` が大きいと誤差が蓄積する可能性があります。
""")